Skip to main content
Logo image

Integrating WeBWorK into Textbooks: Sample Exercises

Robert Beezer, Alex Jordan

Section 2.6 AC in Runestone Test Problems

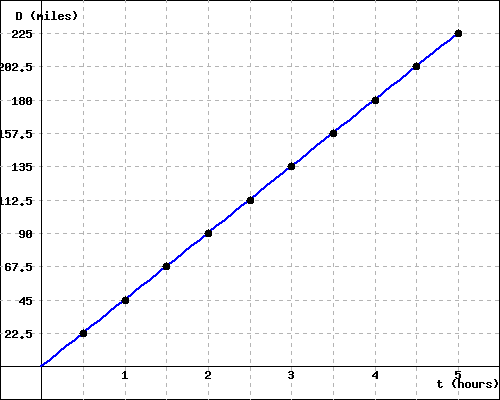
Exploration 2.6.1. Good test problem, scaffolded, dropdown, radio buttons, check that answers restore.

Suppose that the height \(s\) of a ball (in feet) at time \(t\) (in seconds) is given by the formula \(s(t) = 64 - 16(t - 1)^2\text{.}\) This function is graphed below on the interval \(0 \leq t \leq 3\text{.}\)

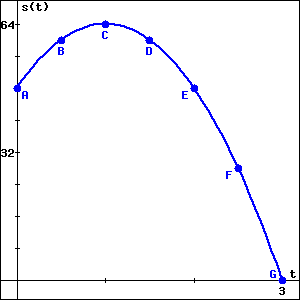
(a) Part a.

Which labeled point (A-G) corresponds to the release of the ball?
How high (in feet) was the ball when it was released?
Which labeled point corresponds to the highest point of the ball?
When (in seconds after being released) did the ball reach its highest point?
Which labeled point corresponds to the ball hitting the ground?
How long (in seconds) after being released did the ball hit the ground?
Answer 1.
\(\text{A}\)
Answer 2.
\(48\)
Answer 3.
\(\text{C}\)
Answer 4.
\(1\)
Answer 5.
\(\text{G}\)
Answer 6.
\(3\)

(b) Part b.

Which option best describes the behavior of the ball on the time interval \(0 \lt t \lt 1\text{?}\)
  • The ball is rising.
  • The ball is falling.
  • The ball changes direction.
  • The ball is released.
  • The ball hits the ground.
Which option best describes the behavior of the ball on the time interval \(1 \lt t \lt 3\text{?}\)
  • The ball is rising.
  • The ball is falling.
  • The ball changes direction.
  • The ball is released.
  • The ball hits the ground.
What occurs at the instant \(t=1\text{?}\)
  • The ball is rising.
  • The ball is falling.
  • The ball changes direction.
  • The ball is released.
  • The ball hits the ground.
Answer 1.
\(\text{The ball is rising.}\)
Answer 2.
\(\text{The ball is falling.}\)
Answer 3.
\(\text{The ball changes direction.}\)

(c) Part c.

Consider the following expression.
\begin{equation*} AV_{[0.5,1]} = \frac{s(1)-s(0.5)}{1-0.5} \end{equation*}
Compute the value of \(AV_{[0.5,1]}\text{.}\)
What does this value measure geometrically?
  • slope. The slope of the line between the points \((0.5, s(0.5)) \) and \((1, s(1)) \text{.}\)
  • curvature. The curvature of the graph of \(s\) on the interval \(0.5 \leq t \leq 1 \text{.}\)
  • area. The area under the graph of \(s\) on the interval \(0.5 \leq t \leq 1 \text{.}\)
  • distance. The distance between the points \((0.5, s(0.5)) \) and \((1, s(1)) \text{.}\)
What does this value measure physically?
  • average velocity. The average velocity of the ball during the interval \(0.5 \leq t \leq 1 \text{.}\)
  • distance. The distance that the ball travels during the interval \(0.5 \leq t \leq 1 \text{.}\)
  • acceleration. The acceleration of the ball during the interval \(0.5 \leq t \leq 1 \text{.}\)
What are the units on \(AV_{[0.5,1]}\text{?}\)
  • feet per second
  • feet
  • seconds
  • feet per second squared
  • foot seconds
  • none of these
Answer 1.
\(8\)
Answer 2.
\(\text{slope}\)
Answer 3.
\(\text{average velocity}\)
Answer 4.
\(\text{feet per second}\)

Exploration 2.6.2. Lots of dropdowns, using NiceTables, check that answers restore.

For each of the indefinite integrals below, the main question is to decide whether the integral can be evaluated using a basic antiderivative, \(u\)-substitution, integration by parts, a combination of \(u\)-substitution and integration by parts, or none of these other techniques.
For integrals for which your answer is affirmative (\(u\)-sub, by parts, combo), you should be able to state what \(u\) and \(du\) are, or what \(u\) and \(dv\) are.
TABLE A
Method
\(\displaystyle \int x^2 \sin(x^3) \, dx\)
  • Basic Integral
  • u-Sub
  • By Parts
  • Combo
  • None of These
\(\displaystyle \int x^2 \sin(x) \, dx\)
  • Basic Integral
  • u-Sub
  • By Parts
  • Combo
  • None of These
\(\displaystyle \int \sin(x^3) \, dx\)
  • Basic Integral
  • u-Sub
  • By Parts
  • Combo
  • None of These
\(\displaystyle \int x^5 \sin(x^3) \, dx\)
  • Basic Integral
  • u-Sub
  • By Parts
  • Combo
  • None of These
TABLE B
Method
\(\displaystyle \int \frac{1}{1+x^2} \, dx\)
  • Basic Integral
  • u-Sub
  • By Parts
  • Combo
  • None of These
\(\displaystyle \int \frac{x}{1+x^2} \, dx\)
  • Basic Integral
  • u-Sub
  • By Parts
  • Combo
  • None of These
\(\displaystyle \int \frac{2x+3}{1+x^2} \, dx\)
  • Basic Integral
  • u-Sub
  • By Parts
  • Combo
  • None of These
\(\displaystyle \int \frac{e^x}{1+(e^x)^2} \, dx\)
  • Basic Integral
  • u-Sub
  • By Parts
  • Combo
  • None of These
TABLE C
Method
\(\displaystyle \int x \ln(x) \, dx\)
  • Basic Integral
  • u-Sub
  • By Parts
  • Combo
  • None of These
\(\displaystyle \int \frac{\ln(x)}{x} \, dx\)
  • Basic Integral
  • u-Sub
  • By Parts
  • Combo
  • None of These
\(\displaystyle \int \ln(1+x^2) \, dx\)
  • Basic Integral
  • u-Sub
  • By Parts
  • Combo
  • None of These
\(\displaystyle \int x\ln(1+x^2) \, dx\)
  • Basic Integral
  • u-Sub
  • By Parts
  • Combo
  • None of These
TABLE D
Method
\(\displaystyle \int x \sqrt{1-x^2} \, dx\)
  • Basic Integral
  • u-Sub
  • By Parts
  • Combo
  • None of These
\(\displaystyle \int \frac{1}{\sqrt{1-x^2}} \, dx\)
  • Basic Integral
  • u-Sub
  • By Parts
  • Combo
  • None of These
\(\displaystyle \int \frac{x}{\sqrt{1-x^2}}\, dx\)
  • Basic Integral
  • u-Sub
  • By Parts
  • Combo
  • None of These
\(\displaystyle \int \frac{1}{x\sqrt{1-x^2}} \, dx\)
  • Basic Integral
  • u-Sub
  • By Parts
  • Combo
  • None of These
Answer 1.
\(\text{u-Sub}\)
Answer 2.
\(\text{By Parts}\)
Answer 3.
\(\text{None of These}\)
Answer 4.
\(\text{Combo}\)
Answer 5.
\(\text{Basic Integral}\)
Answer 6.
\(\text{u-Sub}\)
Answer 7.
\(\text{Combo}\)
Answer 8.
\(\text{u-Sub}\)
Answer 9.
\(\text{By Parts}\)
Answer 10.
\(\text{u-Sub}\)
Answer 11.
\(\text{None of These}\)
Answer 12.
\(\text{Combo}\)
Answer 13.
\(\text{u-Sub}\)
Answer 14.
\(\text{Basic Integral}\)
Answer 15.
\(\text{u-Sub}\)
Answer 16.
\(\text{None of These}\)

Exploration 2.6.3. Old Checkbox macro.

The position of an object moving along a line is given by the function \(s(t)\text{,}\) where \(s\) is measured in feet and \(t\) in seconds. We determine that the velocity is \(v(t) = 4t + 1\) feet per second.
How much does the position change over the time interval \([0,4]\text{?}\)
Change in position = feet
Suppose you are told that the object’s initial position \(s(0) = 7\text{.}\) Determine \(s(2)\text{,}\) the object’s position \(2\) seconds later.
\(s(2) =\)
If you are told instead that the object’s initial position is \(s(0) = 3\text{,}\) what is \(s(2)\text{?}\)
\(s(2) =\)
If we only know the velocity \(v(t)=4t+1\) (but not the initial position), which of the following could be the position function?
Select all that apply.
  • \(\displaystyle s(t) = 2t^2 + t + 37\)
  • \(\displaystyle s(t) = 2t^2 + t\)
  • \(\displaystyle s(t) = 2t^2 + t +5\)
  • \(\displaystyle s(t) = 2t^2 + t +11\)
  • \(\displaystyle s(t) = 2t^2 + t + 20\)
  • None of the above
If, in addition to knowing the velocity function is \(v(t) = 4t+1\text{,}\) we know the initial position \(s(0)\text{,}\) how many possibilities are there for \(s(t)\text{?}\)
  • 0
  • 2
  • 1
  • 5
  • Infinitely many
  • none of the above
Answer 1.
\(36\)
Answer 2.
\(10+7\)
Answer 3.
\(10+3\)
Solution.
\(\int_0^4 4t+1 \, dt = 36\) feet. Therefore, the position function will be \(s_0+ 2t^2+t\text{,}\) where \(s_0\) is the initial velocity.

Exploration 2.6.4. No possible correct answer for dropdown immediately after the first essay box.

Scenario A
In the following scenario, we consider the distribution of a quantity along an axis.
Suppose that the function \(c(x) = 200 + 100 e^{-0.1x}\) models the density of traffic on a straight road, measured in cars per mile, where \(x\) is number of miles east of a major interchange, and consider the definite integral \(\int_0^2 (200 + 100 e^{-0.1x}) \, dx\text{.}\)
(i) What are the units on the product \(c(x) \cdot \triangle x\text{?}\)
Units:
  • cars
  • miles
  • cars/mile
  • miles/car
  • cars*cars
  • miles*miles
(ii) What are the units on the definite integral and its Riemann sum approximation given by
\begin{equation*} \int_0^2 c(x) \, dx \approx \sum_{i=1}^n c(x_i) \triangle x? \end{equation*}
Units:
  • cars
  • miles
  • cars/mile
  • miles/car
  • cars*cars
  • miles*miles
(iii) Evaluate the definite integral \(\int_0^2 c(x) \, dx = \int_0^2 (200 + 100 e^{-0.1x}) \, dx\) and write one sentence to explain the meaning of the value you find.
Scenario B
In the following scenario, we consider the distribution of a quantity along an axis.
On a 6 foot long shelf filled with books, the function \(B\) models the distribution of the weight of the books, measured in pounds per inch, where \(x\) is the number of inches from the left end of the bookshelf. Let \(B(x)\) be given by the rule \(\displaystyle B(x) = 0.5 + \frac{1}{(x+1)^2}\text{.}\)
(i) What are the units on the product \(B(x) \cdot \triangle x\text{?}\)
Units:
  • pounds
  • inches
  • pound/inch
  • inch/pound
  • pound*pound
  • inch*inch
(ii) What are the units on the definite integral and its Riemann sum approximation given by
\begin{equation*} \int_{12}^{36} B(x) \, dx \approx \sum_{i=1}^n B(x_i) \triangle x? \end{equation*}
Units:
  • pounds
  • inches
  • pound/inch
  • inch/pound
  • pound*pound
  • inch*inch
(iii) Evaluate the definite integral \(\displaystyle \int_{0}^{72} B(x) \, dx = \int_0^{72} (0.5 + \frac{1}{(x+1)^2}) \, dx\) and write one sentence to explain the meaning of the value you find.
Answer 1.
\(\text{cars}\)
Answer 2.
\(\text{cars}\)
Answer 3.
Undefined
Answer 4.
\(\text{pounds}\)

Exploration 2.6.5. Hardcoded by Alex, risk of being too long.

Let \(f(x)=\sin(x)\) and let \(T_3(x)=c_0+c_1x+c_2x^2+c_3x^3\text{.}\) Our goal is to find the values of \(c_0,\ldots,c_3\) that make the sine function and its derivative values agree with those of the cubic polynomial \(T_3\) at \(a=0\) and to study the resulting degree \(3\) approximation of the sine function.

(a)

As in previous work, the derivatives of \(T_3(x)\) and their respective values at \(a=0\) are those shown in the following table. Compute the various derivatives of \(f(x)=\sin(x)\) and evaluate them at \(a=0\) accordingly, recording your results in the left side of the table.
\(f(x)=\) \(\sin(x)\) \(T_3(x)=\) \(c_0+c_1x+c_2x^2+c_3x^3\)
\(f'(x)=\) \(T_3'(x)=\) \(c_1+2c_2x+3c_3x^2\)
\(f''(x)=\) \(T_3''(x)=\) \(2c_2+6c_3x\)
\(f'''(x)=\) \(T_3'''(x)=\) \(6c_3\)
\(f(0)=\) \(T_3(0)=\) \(c_0\)
\(f'(0)=\) \(T_3'(0)=\) \(c_1\)
\(f''(0)=\) \(T_3''(0)=\) \(2c_2\)
\(f'''(0)=\) \(T_3'''(0)=\) \(6c_3\)
Answer 1.
\(\cos\!\left(x\right)\)
Answer 2.
\(-\sin\!\left(x\right)\)
Answer 3.
\(-\cos\!\left(x\right)\)
Answer 4.
\(0\)
Answer 5.
\(1\)
Answer 6.
\(0\)
Answer 7.
\(-1\)

(b)

Now, set \(T_3(0)=f(0)\text{,}\) \(T_3'(0)=f'(0)\text{,}\) \(T_3''(0)=f''(0)\text{,}\) and \(T_3'''(0)=f'''(0)\text{.}\) This implies \(c_0={}\), \(c_1={}\), \(c_2={}\), and \(c_3={}\).
Putting it all together, what is the resulting formula for \(T_3(x)\text{?}\)
Answer 1.
\(0\)
Answer 2.
\(1\)
Answer 3.
\(0\)
Answer 4.
\(-{\frac{1}{6}}\)
Answer 5.
\(x-{\frac{1}{6}}x^{3}\)

(c)

Recall that the tangent line approximation \(T_1\) to \(f(x)=\sin(x)\) at \(a=0\) is \(T_1(x)=x\text{,}\) as plotted below. On the same axes, we’ve plotted the cubic approximation \(T_3\) you found in part (b).
What do you observe about the approximation \(T_3\) generates compared to the tangent line approximation \(T_1\text{?}\)
  • The cubic approximation is closer to the function for more values of \(x\text{.}\)
  • The tangent line approximation is closer to the function for more values of \(x\text{.}\)
  • Both approximate the function equally well.
Answer.
\(\text{Choice 1}\)

(d)

Compute \(f(1)-T_1(1)\) and \(f(1)-T_3(1)\text{.}\)
What do you notice about the size and sign of those differences?
Answer 1.
\(-0.158529\)
Answer 2.
\(0.00813765\)

(e)

For about what values of \(x\) does it appear that \(|f(x)-T_1(x)|\lt0.1\text{?}\)
For about what values of \(x\) does it appear that \(|f(x)-T_3(x)|\lt0.1\text{?}\)
Answer 1.
\(\left(-0.9,0.9\right)\)
Answer 2.
\(\left(-1.7,1.7\right)\)

Exercises Exercises

1. Runs the risk of being too long, depending on what students enter.

In this problem, the notation "SIMP(2)" is actually what we have called "SIMP(4)" in our previous work. Different authors use different notation, and the author of this WeBWorK exercise chooses to write "SIMP(n)" where we have written "SIMP(2n)".
Note: for this problem, because later answers depend on earlier ones, you must enter answers for all answer blanks for the problem to be correctly graded. If you would like to get feedback before you completed all computations, enter a "1" for each answer you did not yet compute and then submit the problem. (But note that this will, obviously, result in a problem submission.)
(a) What is the exact value of \(\int_{0}^{5}\,e^x\,dx\text{?}\)
\(\int_{0}^{5}\,e^x\,dx =\)
(b)
Find LEFT(2), RIGHT(2), TRAP(2), MID(2), and SIMP(2); compute the error for each.
LEFT(2) RIGHT(2) TRAP(2) MID(2) SIMP(2)
value
error
(c)
Repeat part (b) with \(n=4\) (instead of \(n=2\)).
LEFT(4) RIGHT(4) TRAP(4) MID(4) SIMP(4)
value
error
(d)
For each rule in part (b), as \(n\) goes from \(n=2\) to \(n=4\text{,}\) does the error go down approximately as you would expect? Explain by calculating the ratios of the errors:
Error LEFT(2)/Error LEFT(4) =
Error RIGHT(2)/Error RIGHT(4) =
Error TRAP(2)/Error TRAP(4) =
Error MID(2)/Error MID(4) =
Error SIMP(2)/Error SIMP(4) =
(Be sure that you can explain in words why these do (or don’t) make sense.)
Answer 1.
\(e^{5}-1\)
Answer 2.
\(2.5\!\left(1+e^{2.5}\right)\)
Answer 3.
\(2.5\!\left(e^{2.5}+e^{5}\right)\)
Answer 4.
\(1.25\!\left(1+2e^{2.5}+e^{5}\right)\)
Answer 5.
\(2.5\!\left(e^{1.25}+e^{3\cdot 1.25}\right)\)
Answer 6.
\(\frac{2\cdot 115.029+217.223}{3}\)
Answer 7.
\(147.413-32.9562\)
Answer 8.
\(147.413-401.489\)
Answer 9.
\(147.413-217.223\)
Answer 10.
\(147.413-115.029\)
Answer 11.
\(147.413-149.094\)
Answer 12.
\(1.25\!\left(1+e^{1.25}+e^{2.5}+e^{3\cdot 1.25}\right)\)
Answer 13.
\(1.25\!\left(e^{1.25}+e^{2.5}+e^{3\cdot 1.25}+e^{5}\right)\)
Answer 14.
\(0.625\!\left(1+2e^{1.25}+2e^{2.5}+2e^{3\cdot 1.25}+e^{5}\right)\)
Answer 15.
\(1.25\!\left(e^{0.625}+e^{3\cdot 0.625}+e^{5\cdot 0.625}+e^{7\cdot 0.625}\right)\)
Answer 16.
\(\frac{2\cdot 138.236+166.126}{3}\)
Answer 17.
\(147.413-73.9924\)
Answer 18.
\(147.413-258.259\)
Answer 19.
\(147.413-166.126\)
Answer 20.
\(147.413-138.236\)
Answer 21.
\(147.413-147.533\)
Answer 22.
\(\frac{114.457}{73.4206}\)
Answer 23.
\(\frac{-254.076}{-110.846}\)
Answer 24.
\(\frac{-69.81}{-18.713}\)
Answer 25.
\(\frac{32.384}{9.177}\)
Answer 26.
\(\frac{-1.681}{-0.12}\)
Solution.
(a) \(\int_{0}^{5}\,e^x\,dx = e^x\bigg|_{0}^{5} = e^5 - e^0 \approx 147.4132\ldots\) (b) Computing the sums directly, since \(\Delta x=2.5\text{,}\) we have LEFT(2) \(= 2.5\cdot e^0 + 2.5\cdot e^{2.5} \approx 32.9563\) RIGHT(2) \(= 2.5\cdot e^{2.5} + 2.5\cdot e^{5} \approx 401.489\) TRAP(2) \(= \frac 1 2 ( 32.9563 + 401.489 ) \approx 217.223\) MID(2) \(= 2.5\cdot e^{1.25} + 2.5\cdot e^{3\cdot 1.25} \approx 115.029\) and SIMP(2) = (2 MID(2) + TRAP(2))/3 \(\approx 149.094\text{.}\) And the errors are just the actual value minus the approximate values, or error(LEFT(2)) = 114.457; error(RIGHT(2)) = -254.076; error(TRAP(2)) = -69.81; error(MID(2)) = 32.3841; and error(SIMP(2)) = -1.681. (c) Similarly, since \(\Delta x = 0.625\text{,}\) we have LEFT(4) = 73.9924; error = 73.4207 RIGHT(4) = 258.259; error = -110.846 TRAP(4) = 166.126; error = -18.713 MID(4) = 138.236; error = 9.177 SIMP(4) = 147.533; error = -0.12. (d) For LEFT and RIGHT, we expect the error to go down by 1/2, and this is very roughly what we see. For MID and TRAP, we expect the error to go down by 1/4, and this is approximately what we see. For SIMP, we expect the error to go down by 1/16, again as observed.

2. Shortened version of question above, but told one student everything was wrong.

Note: for this problem, because later answers depend on earlier ones, you must enter answers for all answer blanks for the problem to be correctly graded. If you would like to get feedback before you completed all computations, enter a "1" for each answer you did not yet compute and then submit the problem. (But note that this will, obviously, result in a problem submission.)
(a) What is the exact value of \(\int_{0}^{5}\,e^x\,dx\text{?}\)
\(\int_{0}^{5}\,e^x\,dx =\)
(b)
Find LEFT(2), RIGHT(2), TRAP(2), MID(2), and SIMP(4); compute the error for each.
LEFT(2) RIGHT(2) TRAP(2) MID(2) SIMP(4)
value
error
(c)
Repeat part (b) with \(n=4\) (instead of \(n=2\)).
LEFT(4) RIGHT(4) TRAP(4) MID(4) SIMP(8)
value
error
Answer 1.
\(e^{5}-1\)
Answer 2.
\(2.5\!\left(1+e^{2.5}\right)\)
Answer 3.
\(2.5\!\left(e^{2.5}+e^{5}\right)\)
Answer 4.
\(1.25\!\left(1+2e^{2.5}+e^{5}\right)\)
Answer 5.
\(2.5\!\left(e^{1.25}+e^{3\cdot 1.25}\right)\)
Answer 6.
\(\frac{2\cdot 115.029+217.223}{3}\)
Answer 7.
\(147.413-32.9562\)
Answer 8.
\(147.413-401.489\)
Answer 9.
\(147.413-217.223\)
Answer 10.
\(147.413-115.029\)
Answer 11.
\(147.413-149.094\)
Answer 12.
\(1.25\!\left(1+e^{1.25}+e^{2.5}+e^{3\cdot 1.25}\right)\)
Answer 13.
\(1.25\!\left(e^{1.25}+e^{2.5}+e^{3\cdot 1.25}+e^{5}\right)\)
Answer 14.
\(0.625\!\left(1+2e^{1.25}+2e^{2.5}+2e^{3\cdot 1.25}+e^{5}\right)\)
Answer 15.
\(1.25\!\left(e^{0.625}+e^{3\cdot 0.625}+e^{5\cdot 0.625}+e^{7\cdot 0.625}\right)\)
Answer 16.
\(\frac{2\cdot 138.236+166.126}{3}\)
Answer 17.
\(147.413-73.9924\)
Answer 18.
\(147.413-258.259\)
Answer 19.
\(147.413-166.126\)
Answer 20.
\(147.413-138.236\)
Answer 21.
\(147.413-147.533\)
Solution.
(a) \(\int_{0}^{5}\,e^x\,dx = e^x\bigg|_{0}^{5} = e^5 - e^0 \approx 147.4132\ldots\) (b) Computing the sums directly, since \(\Delta x=2.5\text{,}\) we have LEFT(2) \(= 2.5\cdot e^0 + 2.5\cdot e^{2.5} \approx 32.9563\) RIGHT(2) \(= 2.5\cdot e^{2.5} + 2.5\cdot e^{5} \approx 401.489\) TRAP(2) \(= \frac 1 2 ( 32.9563 + 401.489 ) \approx 217.223\) MID(2) \(= 2.5\cdot e^{1.25} + 2.5\cdot e^{3\cdot 1.25} \approx 115.029\) and SIMP(4) = (2 MID(2) + TRAP(2))/3 \(\approx 149.094\text{.}\) And the errors are just the actual value minus the approximate values, or error(LEFT(2)) = 114.457; error(RIGHT(2)) = -254.076; error(TRAP(2)) = -69.81; error(MID(2)) = 32.3841; and error(SIMP(4)) = -1.681. (c) Similarly, since \(\Delta x = 0.625\text{,}\) we have LEFT(4) = 73.9924; error = 73.4207 RIGHT(4) = 258.259; error = -110.846 TRAP(4) = 166.126; error = -18.713 MID(4) = 138.236; error = 9.177 SIMP(8) = 147.533; error = -0.12. (d) For LEFT and RIGHT, we expect the error to go down by 1/2, and this is very roughly what we see. For MID and TRAP, we expect the error to go down by 1/4, and this is approximately what we see. For SIMP, we expect the error to go down by 1/16, again as observed.

3. Uses old table macros, but parserCheckboxList.

The graph below shows the distance traveled, \(D\) (in miles) as a function of time, \(t\) (in hours).
(Click on the graph to get a larger version.)
a) For each of the intervals, find the values of \(\Delta D\) and \(\Delta t\) between the indicated start and end times. Enter your answers in their respective columns in the table below.
Time Interval \(\Delta D\) \(\Delta t\)
t = 1 to t = 4
t = 1.5 to t = 3
t = 2 to t = 4
b) Based on your results from (a) it follows that the average rate of change of \(D\) is constant, it does not depend over which interval of time you choose. What is the constant rate of change of \(D\text{?}\)
\(\frac{ \Delta D }{ \Delta t} =\)
c) Which of the statements below CORRECTLY explains the significance of your answer to part (b)? Select ALL that apply (more than one may apply).
  1. It is the total distance the car travels in five hours.
  2. It represents the car’s velocity.
  3. It is the acceleration of the car over the five hour time interval.
  4. It is how far the car will travel in a half-hour.
  5. It is the slope of the line.
  6. It is the average velocity of the car over the first two hours.
  7. None of the above.
Answer 1.
\(135\)
Answer 2.
\(3\)
Answer 3.
\(67.5\)
Answer 4.
\(1.5\)
Answer 5.
\(90\)
Answer 6.
\(2\)
Answer 7.
\(45\)
Answer 8.
\(\text{B, E, F}\)
Solution.
a) Over the first interval \(t = 1\) to \(t = 4\text{,}\) \(\Delta D = 180 - 45 = 135\) and \(\Delta t = 4 - 1 = 3\) .
Similarly, over the second interval \(t = 1.5\) to \(t = 3\text{,}\) \(\Delta D = 135 - 67.5 = 67.5\) and \(\Delta t = 3 - 1.5 = 1.5\) .
Finally, over the last interval \(t = 2\) to \(t = 4\text{,}\) \(\Delta D = 180 - 90 = 90\) and \(\Delta t = 4 - 2 = 2\) .
b) Notice that for each of the three intervals in (a) (as well as any other interval), \(\frac{ \Delta D }{ \Delta t} = 45\text{.}\)
c) There are three correct statements: It represents the car’s velocity, it is the average velocity of the car over the first two hours, and it is the slope of the line.

4. Uses NiceTables.

The figure below shows \(f\text{.}\)
(Click on the graph for a larger version.)
If \(F'=f\) and \(F(0)=0\text{,}\) find \(F(b)\) for \(b=\)1, 2, 3, 4, 5, 6, and fill these values in the following table.
\(b\) 1 2 3 4 5 6
\(F(b)\)
Answer 1.
\(1\)
Answer 2.
\(2\)
Answer 3.
\(2.5\)
Answer 4.
\(2\)
Answer 5.
\(1\)
Answer 6.
\(0.5\)
Solution.
Since \(F(0)=0\text{,}\) \(F(b)=\int_0^{b} f(t)\,dt\text{.}\) For each \(b\) we determine \(F(b)\) graphically: for regions where \(f\) is constant, the integral over that region is just (length)(value of f); for regions that are triangular or trapezoidal, we calculate the area using either of \(\frac12\)(base)(height) (where the height is given by the value of \(f\) and may be negative), or (length)(average height). Thus,
\(F(0)=0\)
\(F(1)= F(0) + 1 = 0 + 1 = 1\)
\(F(2)= F(1) - 0.5 = 1 - 0.5 = 2\)
\(F(3)= F(2) + 0.5 = 2 + 0.5 = 2.5\)
\(F(4)= F(3) - 0.5 = 2.5 - 0.5 = 2\)
\(F(5)= F(4) - 1 = 2 - 1 = 1\)
and, finally,
\(F(6)= F(5) - 0.5 = 1 - 0.5 = 0.5\text{.}\)

5. Units Help, once activated and clicked on.

A rod has length 5 meters. At a distance \(x\) meters from its left end, the density of the rod is given by \(\delta(x)=1 + 2 x\) g/m.
(a) Complete the Riemann sum for the total mass of the rod (use \(Dx\) in place of \(\Delta x\)):
mass = \(\Sigma\)
(b) Convert the Riemann sum to an integral and find the exact mass.
mass =
(include units 1 )
Answer 1.
\(\left(1+2x\right)Dx\)
Answer 2.
\(30\ {\rm g}\)
Solution.
(a) Suppose we choose an \(x\text{,}\) \(0\leq x\leq 5\text{.}\) If \(\Delta x\) is a small fraction of a meter, then the density of the rod is approximately \(\delta(x)\) anywhere from \(x\) to \(x+\Delta x\) meters from the left end of the rod. The mass of the rod from \(x\) to \(x+\Delta x\) meters is therefore approximately \(\delta(x) \Delta x = (1 + 2 x)\Delta x\text{.}\) If we slice the rod into \(N\) pieces, then a Riemann sum is \(\Sigma_{i=1}^{N}(1 + 2 x_i)\Delta x\text{,}\) or, more loosely, \(\Sigma (1 + 2 x)\Delta x\text{.}\) (b) The definite integral is
\begin{equation*} M=\int_0^{5} \delta(x)\,dx = \int_0^{5} (1 + 2 x)\,dx= (1 x + 1 x^2)\bigg|_0^{5} = 30 \hbox{ grams}. \end{equation*}

6. Check Units being Accepted when MathQuill is being used.

The temperature, \(H\text{,}\) in degrees Celsius, of a cup of coffee placed on the kitchen counter is given by \(H = f(t)\text{,}\) where \(t\) is in minutes since the coffee was put on the counter.
  1. Is \(f'(t)\) positive or negative?
    • positive
    • negative
    (Be sure that you are able to give a reason for your answer.)
  2. What are the units of \(f'(10)\text{?}\)
  3. Suppose that \(\lvert f'(10)\rvert = 0.8\) and \(f(10) = 72\text{.}\) Fill in the blanks (including units where needed) and select the appropriate terms to complete the following statement about the temperature of the coffee in this case.
    At minutes after the coffee was put on the counter, its
    • derivative
    • temperature
    • change in temperature
    is and will
    • increase
    • decrease
    by about in the next 30 seconds.
Answer 1.
\(\text{negative}\)
Answer 2.
\({\text{degC/min}}\)
Answer 3.
\(10\)
Answer 4.
\(\text{temperature}\)
Answer 5.
\(72\ {\rm degC}\)
Answer 6.
\(\text{decrease}\)
Answer 7.
\(0.4\ {\rm degC}\)
Solution.
  1. As the cup of coffee cools, the temperature decreases, so \(f'(t)\) is negative.
  2. Since \(f'(t) = dH/dt\text{,}\) the units are degrees Celsius per minute (degC/min).
  3. The quantity \(f'(10)\) represents the rate at which the coffee is cooling, in degrees per minute, 10 minutes after the cup is put on the counter. Thus we can complete the statement:
At 10 minutes after the coffee was put on the counter, its temperature is 72 degC and will decrease by about 0.4 degC in the next 30 seconds.

7. Click on the HelpLink when activated.

For the following indefinite integral, find the full power series centered at \(t=0\) and then give the first 5 nonzero terms of the power series and the open interval of convergence.
\begin{equation*} f(t) = \int \frac{t}{1+t^{5}}\ dt \end{equation*}
\(f(t) = C + \displaystyle\sum\limits_{n=0}^{\infty}\)
\(f(t) = C +\) \(+\) \(+\) \(+\) \(+\) \(+ \cdots\)
The open interval of convergence is: (Give your answer in interval notation 2 .)
Answer 1.
\(\frac{\left(-1\right)^{n}t^{5n+2}}{5n+2}\)
Answer 2.
\(\frac{t^{5\cdot 0+2}}{5\cdot 0+2}\)
Answer 3.
\(\frac{-1t^{5\cdot 1+2}}{5\cdot 1+2}\)
Answer 4.
\(\frac{t^{5\cdot 2+2}}{5\cdot 2+2}\)
Answer 5.
\(\frac{-1t^{5\cdot 3+2}}{5\cdot 3+2}\)
Answer 6.
\(\frac{t^{5\cdot 4+2}}{5\cdot 4+2}\)
Answer 7.
\(\left(-1,1\right)\)

8. Weird Error in the Static Rendering.

Match the following equations with their direction field. Clicking on each picture will give you an enlarged view. While you can probably solve this problem by guessing, it is useful to try to predict characteristics of the direction field and then match them to the picture.
Here are some handy characteristics to start with -- you will develop more as you practice.
  1. Set \(y\) equal to zero and look at how the derivative behaves along the \(x\)-axis.
  2. Do the same for the \(y\)-axis by setting \(x\) equal to \(0\)
  3. Consider the curve in the plane defined by setting \(y'=0\) -- this should correspond to the points in the picture where the slope is zero.
  4. Setting \(y'\) equal to a constant other than zero gives the curve of points where the slope is that constant. These are called isoclines, and can be used to construct the direction field picture by hand.
  1. \(\displaystyle \displaystyle y'= -\frac{(2x+y)}{(2y)}\)
  2. \(\displaystyle \displaystyle y'= \frac{y}{x} +3\cos(2x)\)
  3. \(\displaystyle y'= y + xe^{-x} + 1\)
  4. \(\displaystyle y'= 2\sin(3x) + 1 + y\)
Error: PGbasicmacros: imageRow: Unknown displayMode: PTX.
Error: PGbasicmacros: imageRow: Unknown displayMode: PTX.

9. My note only said weird... not sure why.

Given the differential equation \(x'(t) = - x^4 + 1x^3 + 13x^2 - 12.25x - 9.1875\text{.}\)
List the constant (or equilibrium) solutions to this differential equation in increasing order and indicate whether or not these equilibria are stable, semi-stable, or unstable. (It helps to sketch the graph. 3  )
  • stable
  • unstable
  • semi-stable
  • stable
  • unstable
  • semi-stable
  • stable
  • unstable
  • semi-stable
  • stable
  • unstable
  • semi-stable
Answer 1.
\(-3.5\)
Answer 2.
\(-0.5\)
Answer 3.
\(1.5\)
Answer 4.
\(3.5\)

10. Problem changes after hitting submit.

Calculate the integral:
\(\displaystyle \int \frac{1}{(x+6)(x+8)}\,dx =\)
Answer.
\(0.5\ln\!\left(\left|x+6\right|\right)-0.5\ln\!\left(\left|x+8\right|\right)+C\)
Solution.
\begin{equation*} \frac{1}{(x+6)(x+8)}=\frac{A}{x+6}+\frac{B}{x+8}, \end{equation*}
giving
\begin{equation*} 1 = A(x+8)+B(x+6), \end{equation*}
or
\begin{equation*} 1 = (A+B)x+ (8 A+6 B). \end{equation*}
Solving for \(A\) and \(B\text{,}\) we find \(A = 0.5\) and \(B = -0.5\text{,}\) so
\begin{equation*} \int \frac{1}{(x+6)(x+8)}\,dx= \int\frac{0.5}{x+6}\,dx + \int \frac{-0.5}{x+8}\,dx = 0.5\ln\!\left(\left|x+6\right|\right)-0.5\ln\!\left(\left|x+8\right|\right)+C. \end{equation*}

11. Another problem that changes after hitting submit.

Find the volume of the solid obtained by rotating the region in the first quadrant bounded by \(y=x^{6}\text{,}\) \(y=1\text{,}\) and the \(y\)-axis around the \(y\)-axis.
Volume =
Answer.
\(2.35619449019234\)
Solution.
\(\Delta y\) and radius \(x=\root 6\of{y}\text{.}\) Thus
\begin{equation*} \hbox{Volume of slice }\approx \pi x^2\Delta y =\pi y^{1/3}\,\Delta y, \end{equation*}
and
\begin{equation*} \hbox{Volume of solid } = \lim_{\Delta y\to 0}\Sigma\pi y^{1/3}\,\Delta y = \int_0^1 \pi y^{1/3}\, dy \end{equation*}
\begin{equation*} = {3 \pi\over 4} y^{1 + 1/3}\bigg|_0^1 = {3 \pi\over 4}. \end{equation*}
PrevTopNext
Feedback